CHSPy (Cubic Hermite Splines for Python)¶
This module provides Python tools for cubic Hermite splines with one argument (time) and multiple values (\(ℝ→ℝ^n\)). It was branched of from JiTCDDE, which uses it for representing the past of a delay differential equation. CHSPy is not optimised for efficiency, however it should be fairly effective for high-dimensionally valued splines.
Each spline (CubicHermiteSpline) is stored as a series of anchors (using the Anchor class) each of which contains:
a time point (
time),an \(n\)-dimensional state (
state),an \(n\)-dimensional temporal derivative (
diff).
Between such anchors, the spline is uniquely described by a polynomial of third degree. With other words, the spline is a piecewise cubic Hermite interpolant of its anchors.
Example¶
The following example implements a simple three-dimensional spline with three anchors (at \(t=0\), \(t=1\), and \(t=4\)) and plots it.
from chspy import CubicHermiteSpline
from matplotlib.pyplot import subplots
spline = CubicHermiteSpline(n=3)
# time state slope
spline.add(( 0 , [1,3,0], [0,1,0] ))
spline.add(( 1 , [3,2,0], [0,4,0] ))
spline.add(( 4 , [0,1,3], [0,4,0] ))
fig,axes = subplots(figsize=(7,2))
spline.plot(axes)
axes.set_xlabel("time")
axes.set_ylabel("state")
fig.legend(loc="right",labelspacing=1)
fig.subplots_adjust(right=0.7)
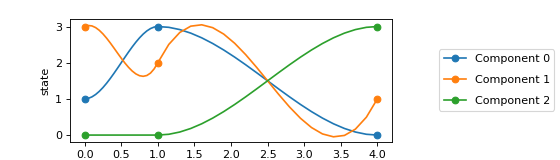
The markers depict the anchors. Note how the slope at the anchors is zero for Components 0 and 2 (which is how we defined the spline), while it isn’t for Component 1.
Command Reference¶
- class Anchor(time, state, diff)¶
Class for a single anchor. Behaves mostly like a tuple, except that the respective components can also be accessed via the attributes
time,state, anddiff, and some copying and checks are performed upon creation. Also, it implements the less-than operator (<) for comparison by time, which allows to use Python’s sort routines.
- interpolate(t, i, anchors)¶
Returns the
i-th value of a cubic Hermite interpolant of theanchorsat timet.
- interpolate_vec(t, anchors)¶
Returns all values of a cubic Hermite interpolant of the
anchorsat timet.
- interpolate_diff(t, i, anchors)¶
Returns the
i-th component of the derivative of a cubic Hermite interpolant of theanchorsat timet.
- interpolate_diff_vec(t, anchors)¶
Returns the derivative of a cubic Hermite interpolant of the
anchorsat timet.
- norm_sq_interval(anchors, indices)¶
Returns the squared norm of the interpolant of
anchorsfor theindices.
- norm_sq_partial(anchors, indices, start)¶
Returns the sqared norm of the interpolant of
anchorsfor theindices, but only taking into account the time afterstart.
- scalar_product_interval(anchors, indices_1, indices_2)¶
Returns the (integral) scalar product of the interpolants of
anchorsforindices_1(one side of the product) andindices_2(other side).
- scalar_product_partial(anchors, indices_1, indices_2, start)¶
Returns the scalar product of the interpolants of
anchorsforindices_1(one side of the product) andindices_2(other side), but only taking into account the time afterstart.
- class Extrema(n)¶
Class for containing the extrema and their positions in
ndimensions. These can be accessed via the attributesminima,maxima,arg_min, andarg_max.- update(times, values, condition=True)¶
Updates the extrema if
valuesare more extreme.- Parameters:
- conditionboolean or array of booleans
Only the components where this is
Trueare updated.
- extrema_from_anchors(anchors, beginning=None, end=None, target=None)¶
Finds minima and maxima of the Hermite interpolant for the anchors.
- Parameters:
- beginningfloat or
None Beginning of the time interval for which extrema are returned. If
None, the time of the first anchor is used.- endfloat or
None End of the time interval for which extrema are returned. If
None, the time of the last anchor is used.- targetExtrema or
None If an Extrema instance, this one is updated with the newly found extrema and also returned (which means that newly found extrema will be ignored when the extrema in
targetare more extreme).
- beginningfloat or
- Returns:
- extrema: Extrema object
An
Extremainstance containing the extrema and their positions.
- solve_from_anchors(anchors, i, value, beginning=None, end=None)¶
Finds the times at which a component of the Hermite interpolant for the anchors assumes a given value and the derivatives at those points (allowing to distinguish upwards and downwards threshold crossings).
- Parameters:
- iinteger
The index of the component.
- valuefloat
The value that shall be assumed
- beginningfloat or
None Beginning of the time interval for which positions are returned. If
None, the time of the first anchor is used.- endfloat or
None End of the time interval for which positions are returned. If
None, the time of the last anchor is used.
- Returns:
- positionslist of pairs of floats
Each pair consists of a time where
valueis assumed and the derivative (ofcomponent) at that time.
- class CubicHermiteSpline(n=None, anchors=())¶
Class for a cubic Hermite Spline of one variable (time) with
nvalues. This behaves like a list with additional functionalities and checks. Note that the times of the anchors must always be in ascending order.- Parameters:
- ninteger
Dimensionality of the values. If
None, the following argument must be an instance of CubicHermiteSpline.- anchorsiterable of triplets
Contains all the anchors with which the spline is initiated. If
nisNoneand this is an instance of CubicHermiteSpline, all properties are copied from it.
- append(anchor)¶
Append object to the end of the list.
- extend(anchors)¶
Extend list by appending elements from the iterable.
- copy()¶
Return a shallow copy of the list.
- insert(key, item)¶
Insert object before index.
- sort()¶
Sort the list in ascending order and return None.
The sort is in-place (i.e. the list itself is modified) and stable (i.e. the order of two equal elements is maintained).
If a key function is given, apply it once to each list item and sort them, ascending or descending, according to their function values.
The reverse flag can be set to sort in descending order.
- add(anchor)¶
Inserts
anchorat the appropriate time.
- pop(index=-1)¶
Remove and return item at index (default last).
Raises IndexError if list is empty or index is out of range.
- remove(value)¶
Remove first occurrence of value.
Raises ValueError if the value is not present.
- clear_from(n)¶
Removes all anchors with an index of
nor higher.
- clear()¶
Remove all items from list.
- reverse()¶
Reverse IN PLACE.
- property t¶
The time of the last anchor. This may be overwritten in subclasses such that
self.tand the time of the last anchor are not identical anymore.
- property times¶
The times of all anchors.
- last_index_before(time)¶
Returns the index of the last anchor before
time. Returns 0 iftimeis before the first anchor.
- first_index_after(time)¶
Returns the index of the first anchor after
time. Iftimeis after the last anchors, the latter’s index is returned.
- constant(state, time=0)¶
makes the spline constant, removing possibly previously existing anchors.
- Parameters:
- stateiterable of floats
- timefloat
The time of the last point.
- from_function(function, times_of_interest=None, max_anchors=100, tol=5)¶
Like
from_funcexcept for not being a class method and overwriting previously existing anchors. In most cases, you want to usefrom_funcinstead.
- classmethod from_func(function, times_of_interest=None, max_anchors=100, tol=5)¶
makes the spline interpolate a given function at heuristically determined points. More precisely, starting with
times_of_interest, anchors are added until either:anchors are closer than the tolerance
the value of an anchor is approximated by the interpolant of its neighbours within the tolerance
the maximum number of anchors is reached.
This removes possibly previously existing anchors.
- Parameters:
- functioncallable or iterable of SymPy/SymEngine expressions
The function to be interpolated. If callable, this is interpreted like a regular function mapping a time point to a state vector (as an iterable). If an iterable of expressions, each expression represents the respective component of the function.
- times_of_interestiterable of numbers
Initial set of time points considered for the interpolation. All created anhcors will between the minimal and maximal timepoint.
- max_anchorspositive integer
The maximum number of anchors that this routine will create (including those for the
times_of_interest).- tolinteger
This is a parameter for the heuristics, more precisely the number of digits considered for tolerance in several places.
- classmethod from_data(times, states)¶
Creates a new cubic Hermite spline based on a provided dataset. The derivative of a given anchor is estimated from a quadratic interpolation of that anchor and the neighbouring ones. (For the first and last anchor, it’s only a linear interpolation.)
This is only a best general guess how to interpolate the data. Often you can apply your knowledge of the data to do better.
- Parameters:
- timesarray-like
The times of the data points.
- statesarray-like
The values of the data. The first dimension has to have the same length as
times.
- get_anchors(time)¶
Find the two anchors neighbouring
time. Iftimeis outside the ranges of times covered by the anchors, return the two nearest anchors.
- get_state(times)¶
Get the state of the spline at
times. If any time point lies outside of the anchors, the state will be extrapolated.
- get_recent_state(t)¶
Interpolate the state at time
tfrom the last two anchors. This usually only makes sense iftlies between the last two anchors.
- forget(delay)¶
Remove all anchors that are “out of reach” of the delay with respect to
self.t.
- extrema(beginning=None, end=None)¶
Returns the positions and values of the minima and maxima of the spline (for each component) within the specified time interval.
- Parameters:
- beginningfloat or
None Beginning of the time interval for which extrema are returned. If
None, the time of the first anchor is used.- endfloat or
None End of the time interval for which extrema are returned. If
None, the time of the last anchor is used.
- beginningfloat or
- Returns:
- extrema: Extrema object
An
Extremainstance containing the extrema and their positions.
- solve(i, value, beginning=None, end=None)¶
Finds the times at which a component of the spline assumes a given value and the derivatives at those points (allowing to distinguish upwards and downwards threshold crossings). This will not work well if the spline is constantly at the given value for some interval.
- Parameters:
- iinteger
The index of the component.
- valuefloat
The value that shall be assumed
- beginningfloat or
None Beginning of the time interval for which solutions are returned. If
None, the time of the first anchor is used.- endfloat or
None End of the time interval for which solutions are returned. If
None, the time of the last anchor is used.
- Returns:
- positionslist of pairs of floats
Each pair consists of a time where
valueis assumed and the derivative (ofcomponent) at that time.
- norm(delay, indices)¶
Computes the norm of the spline for the given indices taking into account the time between
self.t−delayandself.t.
- scalar_product(delay, indices_1, indices_2)¶
Computes the scalar product of the spline between
indices_1(one side of the product) andindices_2(other side) taking into account the time betweenself.t−delayandself.t.
- scale(indices, factor)¶
Scales the spline for
indicesbyfactor.
- subtract(indices_1, indices_2, factor)¶
Substract the spline for
indices_2multiplied byfactorfrom the spline forindices_1.
- interpolate_anchor(time)¶
Interpolates an anchor at
time.
- truncate(time)¶
Interpolates an anchor at
timeand removes all later anchors.
- plus(other)¶
Sum with another spline in place. If the other spline has an anchor that does not have the time of an existing anchor, a new anchor will be added at this time.
- plot(axes, components='all', resolution=20, *args, **kwargs)¶
Plots the interpolant onto the provided Matplotlib axes object. If
componentsisNone, all components are plotted at once. Otherwise only the selected component is plotted. By default this callsplotwithmarkevery=resolution(marking the anchors) andmarker="o", but you can override those arguments. It will also label each component withf"Component {i}". All further arguments are forwarded to Matplotlib’splot.- Parameters:
- componentsint, iterable of ints, or “all”
Which components should be plotted. If
"all", all components will be plotted.- resolutionint
How often the Hermite polynomial should be evaluated for plotting between each anchor. The higher this number, the more accurate the plot.
- match_anchors(*splines)¶
Ensure that splines have anchors at the same times, interpolating intermediate anchors if necessary. All of this happens in place.
- join(*splines)¶
Glues the splines together along the value dimension, i.e., returns a new spline that features the input splines as disjoint subsets of its components.