CHSPy (Cubic Hermite Splines for Python)

This module provides Python tools for cubic Hermite splines with one argument (time) and multiple values (\(ℝ→ℝ^n\)). It was branched of from JiTCDDE, which uses it for representing the past of a delay differential equation. CHSPy is not optimised for efficiency, however it should be fairly effective for high-dimensionally valued splines.

Each spline (CubicHermiteSpline) is stored as a series of anchors (using the Anchor class) each of which contains:

• a time point (time),

• an \(n\)-dimensional state (state),

• an \(n\)-dimensional temporal derivative (diff).

Between such anchors, the spline is uniquely described by a polynomial of third degree. With other words, the spline is a piecewise cubic Hermite interpolant of its anchors.

Example

The following example implements a simple three-dimensional spline with three anchors (at \(t=0\), \(t=1\), and \(t=4\)) and plots it.

from chspy import CubicHermiteSpline
from matplotlib.pyplot import subplots

spline = CubicHermiteSpline(n=3)

#            time   state    slope
spline.add((   0 , [1,3,0], [0,1,0] ))
spline.add((   1 , [3,2,0], [0,4,0] ))
spline.add((   4 , [0,1,3], [0,4,0] ))

fig,axes = subplots(figsize=(7,2))
spline.plot(axes)
axes.set_xlabel("time")
axes.set_ylabel("state")
fig.legend(loc="right",labelspacing=1)
fig.subplots_adjust(right=0.7)

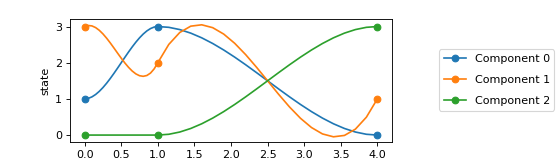
The markers depict the anchors. Note how the slope at the anchors is zero for Components 0 and 2 (which is how we defined the spline), while it isn’t for Component 1.

Command Reference

class Anchor(time, state, diff)

Class for a single anchor. Behaves mostly like a tuple, except that the respective components can also be accessed via the attributes time, state, and diff, and some copying and checks are performed upon creation. Also, it implements the less-than operator (<) for comparison by time, which allows to use Python’s sort routines.

interpolate(t, i, anchors)

Returns the i-th value of a cubic Hermite interpolant of the anchors at time t.

interpolate_vec(t, anchors)

Returns all values of a cubic Hermite interpolant of the anchors at time t.

interpolate_diff(t, i, anchors)

Returns the i-th component of the derivative of a cubic Hermite interpolant of the anchors at time t.

interpolate_diff_vec(t, anchors)

Returns the derivative of a cubic Hermite interpolant of the anchors at time t.

norm_sq_interval(anchors, indices)

Returns the squared norm of the interpolant of anchors for the indices.

norm_sq_partial(anchors, indices, start)

Returns the sqared norm of the interpolant of anchors for the indices, but only taking into account the time after start.

scalar_product_interval(anchors, indices_1, indices_2)

Returns the (integral) scalar product of the interpolants of anchors for indices_1 (one side of the product) and indices_2 (other side).

scalar_product_partial(anchors, indices_1, indices_2, start)

Returns the scalar product of the interpolants of anchors for indices_1 (one side of the product) and indices_2 (other side), but only taking into account the time after start.

class Extrema(n)

Class for containing the extrema and their positions in n dimensions. These can be accessed via the attributes minima, maxima, arg_min, and arg_max.

update(times, values, condition=True)

Updates the extrema if values are more extreme.

Parameters:

conditionboolean or array of booleans

Only the components where this is True are updated.

extrema_from_anchors(anchors, beginning=None, end=None, target=None)

Finds minima and maxima of the Hermite interpolant for the anchors.

Parameters:

beginningfloat or None

Beginning of the time interval for which extrema are returned. If None, the time of the first anchor is used.

endfloat or None

End of the time interval for which extrema are returned. If None, the time of the last anchor is used.

targetExtrema or None

If an Extrema instance, this one is updated with the newly found extrema and also returned (which means that newly found extrema will be ignored when the extrema in target are more extreme).

Returns:

extrema: Extrema object

An Extrema instance containing the extrema and their positions.

solve_from_anchors(anchors, i, value, beginning=None, end=None)

Finds the times at which a component of the Hermite interpolant for the anchors assumes a given value and the derivatives at those points (allowing to distinguish upwards and downwards threshold crossings).

Parameters:

iinteger

The index of the component.

valuefloat

The value that shall be assumed

beginningfloat or None

Beginning of the time interval for which positions are returned. If None, the time of the first anchor is used.

endfloat or None

End of the time interval for which positions are returned. If None, the time of the last anchor is used.

Returns:

positionslist of pairs of floats

Each pair consists of a time where value is assumed and the derivative (of component) at that time.

class CubicHermiteSpline(n=None, anchors=())

Class for a cubic Hermite Spline of one variable (time) with n values. This behaves like a list with additional functionalities and checks. Note that the times of the anchors must always be in ascending order.

Parameters:

ninteger

Dimensionality of the values. If None, the following argument must be an instance of CubicHermiteSpline.

anchorsiterable of triplets

Contains all the anchors with which the spline is initiated. If n is None and this is an instance of CubicHermiteSpline, all properties are copied from it.

append(anchor)

Append object to the end of the list.

extend(anchors)

Extend list by appending elements from the iterable.

copy()

Return a shallow copy of the list.

insert(key, item)

Insert object before index.

sort()

Sort the list in ascending order and return None.

The sort is in-place (i.e. the list itself is modified) and stable (i.e. the order of two equal elements is maintained).

If a key function is given, apply it once to each list item and sort them, ascending or descending, according to their function values.

The reverse flag can be set to sort in descending order.

add(anchor)

Inserts anchor at the appropriate time.

pop(index=-1)

Remove and return item at index (default last).

Raises IndexError if list is empty or index is out of range.

remove(value)

Remove first occurrence of value.

Raises ValueError if the value is not present.

clear_from(n)

Removes all anchors with an index of n or higher.

clear()

Remove all items from list.

reverse()

Reverse IN PLACE.

property t

The time of the last anchor. This may be overwritten in subclasses such that self.t and the time of the last anchor are not identical anymore.

property times

The times of all anchors.

last_index_before(time)

Returns the index of the last anchor before time. Returns 0 if time is before the first anchor.

first_index_after(time)

Returns the index of the first anchor after time. If time is after the last anchors, the latter’s index is returned.

constant(state, time=0)

makes the spline constant, removing possibly previously existing anchors.

Parameters:

stateiterable of floats

timefloat

The time of the last point.

from_function(function, times_of_interest=None, max_anchors=100, tol=5)

Like from_func except for not being a class method and overwriting previously existing anchors. In most cases, you want to use from_func instead.

classmethod from_func(function, times_of_interest=None, max_anchors=100, tol=5)

makes the spline interpolate a given function at heuristically determined points. More precisely, starting with times_of_interest, anchors are added until either:

• anchors are closer than the tolerance

• the value of an anchor is approximated by the interpolant of its neighbours within the tolerance

• the maximum number of anchors is reached.

This removes possibly previously existing anchors.

Parameters:

functioncallable or iterable of SymPy/SymEngine expressions

The function to be interpolated. If callable, this is interpreted like a regular function mapping a time point to a state vector (as an iterable). If an iterable of expressions, each expression represents the respective component of the function.

times_of_interestiterable of numbers

Initial set of time points considered for the interpolation. All created anhcors will between the minimal and maximal timepoint.

max_anchorspositive integer

The maximum number of anchors that this routine will create (including those for the times_of_interest).

tolinteger

This is a parameter for the heuristics, more precisely the number of digits considered for tolerance in several places.

classmethod from_data(times, states)

Creates a new cubic Hermite spline based on a provided dataset. The derivative of a given anchor is estimated from a quadratic interpolation of that anchor and the neighbouring ones. (For the first and last anchor, it’s only a linear interpolation.)

This is only a best general guess how to interpolate the data. Often you can apply your knowledge of the data to do better.

Parameters:

timesarray-like

The times of the data points.

statesarray-like

The values of the data. The first dimension has to have the same length as times.

get_anchors(time)

Find the two anchors neighbouring time. If time is outside the ranges of times covered by the anchors, return the two nearest anchors.

get_state(times)

Get the state of the spline at times. If any time point lies outside of the anchors, the state will be extrapolated.

get_recent_state(t)

Interpolate the state at time t from the last two anchors. This usually only makes sense if t lies between the last two anchors.

forget(delay)

Remove all anchors that are “out of reach” of the delay with respect to self.t.

extrema(beginning=None, end=None)

Returns the positions and values of the minima and maxima of the spline (for each component) within the specified time interval.

Parameters:

beginningfloat or None

Beginning of the time interval for which extrema are returned. If None, the time of the first anchor is used.

endfloat or None

End of the time interval for which extrema are returned. If None, the time of the last anchor is used.

Returns:

extrema: Extrema object

An Extrema instance containing the extrema and their positions.

solve(i, value, beginning=None, end=None)

Finds the times at which a component of the spline assumes a given value and the derivatives at those points (allowing to distinguish upwards and downwards threshold crossings). This will not work well if the spline is constantly at the given value for some interval.

Parameters:

iinteger

The index of the component.

valuefloat

The value that shall be assumed

beginningfloat or None

Beginning of the time interval for which solutions are returned. If None, the time of the first anchor is used.

endfloat or None

End of the time interval for which solutions are returned. If None, the time of the last anchor is used.

Returns:

positionslist of pairs of floats

Each pair consists of a time where value is assumed and the derivative (of component) at that time.

norm(delay, indices)

Computes the norm of the spline for the given indices taking into account the time between self.t − delay and self.t.

scalar_product(delay, indices_1, indices_2)

Computes the scalar product of the spline between indices_1 (one side of the product) and indices_2 (other side) taking into account the time between self.t − delay and self.t.

scale(indices, factor)

Scales the spline for indices by factor.

subtract(indices_1, indices_2, factor)

Substract the spline for indices_2 multiplied by factor from the spline for indices_1.

interpolate_anchor(time)

Interpolates an anchor at time.

truncate(time)

Interpolates an anchor at time and removes all later anchors.

plus(other)

Sum with another spline in place. If the other spline has an anchor that does not have the time of an existing anchor, a new anchor will be added at this time.

plot(axes, components='all', resolution=20, *args, **kwargs)

Plots the interpolant onto the provided Matplotlib axes object. If components is None, all components are plotted at once. Otherwise only the selected component is plotted. By default this calls plot with markevery=resolution (marking the anchors) and marker="o", but you can override those arguments. It will also label each component with f"Component {i}". All further arguments are forwarded to Matplotlib’s plot.

Parameters:

componentsint, iterable of ints, or “all”

Which components should be plotted. If "all", all components will be plotted.

resolutionint

How often the Hermite polynomial should be evaluated for plotting between each anchor. The higher this number, the more accurate the plot.

match_anchors(*splines)

Ensure that splines have anchors at the same times, interpolating intermediate anchors if necessary. All of this happens in place.

join(*splines)

Glues the splines together along the value dimension, i.e., returns a new spline that features the input splines as disjoint subsets of its components.